Math- How to Simplify and Solve Radicals and Square Roots

Roots" (or "radicals") are the "opposite" operation of applying exponents; you can "undo" a power with a radical, and a radical can "undo" a power. For instance, if you square 2, you get 4, and if you "take the square root of 4", you get 2; if you square 3, you get 9, and if you "take the square root of 9", you get 3:   Copyright © Elizabeth Stapel 1999-2011 All Rights Reserved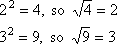

The "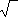" symbol is called the "radical"symbol. (Technically, just the "check mark" part of the symbol is the radical; the line across the top is called the "vinculum".) The expression "  " is read as "root nine", "radical nine", or "the square root of nine".You can raise numbers to powers other than just 2; you can cube things, raise them to the fourth power, raise them to the 100th power, and so forth. In the same way, you can take the cube root of a number, the fourth root, the 100th root, and so forth. To indicate some root other than a square root, you use the same radical symbol, but you insert a number into the radical, tucking it into the "check mark" part. For instance: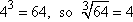

The "3" in the above is the "index" of the radical; the "64" is "the argument of the radical", also called "the radicand". Since most radicals you see are square roots, the index is not included on square roots. While " 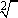 " would be technically correct, I've never seen it used.

	ADVERTISEMENT

a square (second) root is written as 

a cube (third) root is written as 

a fourth root is written as  

a fifth root is written as:  

You can take any counting number, square it, and end up with a nice neat number. But the process doesn't always work going backwards. For instance, consider , the square root of three. There is no nice neat number that squares to 3, so  cannot be simplified as a nice whole number. You can deal with  in either of two ways: If you are doing a word problem and are trying to find, say, the rate of speed, then you would grab your calculator and find the decimal approximation of :

Then you'd round the above value to an appropriate number of decimal places and use a real-world unit or label, like "1.7 ft/sec". On the other hand, you may be solving a plain old math exercise, something with no "practical" application. Then they would almost certainly want the "exact" value, so you'd give your answer as being simply "".